Writing Equations Of Circles Worksheet Answers
EQUATIONS OF CIRCLES WORKSHEET
Problem 1 :
Write the standard equation of the circle whose center is (-4, 0) and radius is 7.
Problem 2 :
Write the standard equation of the circle whose general equation is
x 2 + y 2 - 4x + 6y - 12 = 0
Problem 3 :
The point (1 ,2) is on a circle whose center is (5, -1). Write the standard equation of the circle.
Problem 4 :
The equation of a circle is
(x + 2) 2 + (y - 3) 2 = 9
Graph the circle.
Problem 5 :
A bank of lights is arranged over a stage. Each light illuminates a circular area on the stage. A coordinate plane is used to arrange the lights, using the corner of stage as the origin. The equation(x - 13) 2 + (y - 4) 2 = 16 represents one of the disks of light.
(i) Graph the disk of light.
(ii) Three actors are located as follows :
Henry is at (11, 4)
Jolene is at (8, 5)
Martin is at (15, 5)
Which actors are in the disk of light ?

Detailed Answer Key
Problem 1 :
Write the standard equation of the circle whose center is (-4, 0) and radius is 7.
Solution :
Standard equation of a circle.
(x - h) 2 + (y - k) 2 = r 2
Plug (h, k) = (-4, 0) and r = 7.
[x - (-4) 2 ] + (y - 0) 2 = 7 2
Simplify.
(x + 4)2 + y2 = 49
Problem 2 :
Write the standard equation of the circle whose general equation is
x 2 + y 2 - 4x + 6y - 12 = 0
Solution :
To find the standard equation of the circle, we need to know the center and radius.
Let us find the center and radius from the given general equation of the circle.
Comparing
x 2 + y 2 + 2gx + 2fy + c = 0
and
x 2 + y 2 - 4x + 6y - 12 = 0,
we have
2g = - 4 -----> g = -2
2f = 6 -----> f = 3
c = -12
Center = (-g, -f) = (2, -3)
Radius = √[g2 + f2 - c]
Radius = √[(-2) 2 + 3 2 - (-12)]
Radius = √[4 + 9 + 12]
Radius = √25
Radius = 5
Standard equation of a circle :
(x - h) 2 + (y - k) 2 = r 2
Plug (h, k) = (2, -3) and r = 5.
(x - 2) 2 + [y - (-3) 2 ] = 5 2
Simplify.
(x - 2) 2 + (y + 3) 2 = 25
Problem 3 :
The point (1 ,2) is on a circle whose center is (5, -1). Write the standard equation of the circle.
Solution :
To find the standard equation of the circle, we need to know the center and radius.The center is already given and we need to find the radius.
Using distance formula, we have
Radius = √[(5 - 1)2 + (-1 - 2)2 ]
Radius = √[42 + (-3)2]
Radius = √[16 + 9]
Radius = √25
Radius = 5
Standard equation of a circle :
(x - h) 2 + (y - k) 2 = r 2
Plug (h, k) = (5, -1) and r = 5.
(x - 5) 2 + [y - (-1) 2 ] = 5 2
Simplify.
(x - 5) 2 + (y + 1) 2 = 5 2
Problem 4 :
The equation of a circle is
(x + 2) 2 + (y - 3) 2 = 9
Graph the circle.
Solution :
To graph a circle, we need to know the radius and center of the circle.
Rewrite the equation to find the center and radius.
(x + 2) 2 + (y - 3) 2 = 9
[x - (-2) 2 ] + (y - 3) 2 = 32
So, the center is (-2, 3) and the radius is 3.
To graph the circle, place the point of a compass at (-2, 3), set the radius at 3 units and swing the compass to draw a full circle.
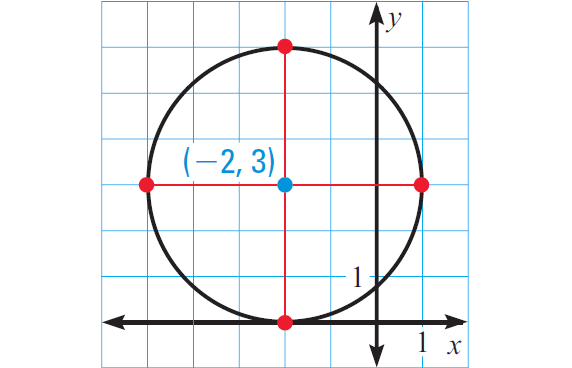
Problem 5 :
A bank of lights is arranged over a stage. Each light illuminates a circular area on the stage. A coordinate plane is used to arrange the lights, using the corner of stage as the origin. The equation(x - 13) 2 + (y - 4) 2 = 16 represents one of the disks of light.
(i) Graph the disk of light.
(ii) Three actors are located as follows :
Henry is at (11, 4)
Jolene is at (8, 5)
Martin is at (15, 5)
Which actors are in the disk of light ?
Solution :
Solution (i) :
To graph the disk of light, we need to know the center and radius of the circle.
Rewrite the equation to find the center and radius.
(x - 13) 2 + (y - 4) 2 = 16
(x - 13) 2 + (y - 4) 2 = 42
So, the center is (13, 4) and the radius is 4.
The circle with center at (13, 4) and radius 4 units shown below (Graph of the disk of light).
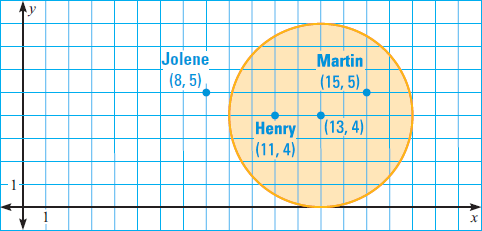
Solution (ii) :
The graph given above shows that Henry and Martin are both in the disk of light.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
HCF and LCM word problems
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Algebra word problems
Word problems on trains
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on unit price
Word problems on unit rate
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Double facts word problems
Trigonometry word problems
Percentage word problems
Profit and loss word problems
Markup and markdown word problems
Decimal word problems
Word problems on fractions
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Time and work word problems
Word problems on sets and venn diagrams
Word problems on ages
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Profit and loss shortcuts
Percentage shortcuts
Times table shortcuts
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
Writing Equations Of Circles Worksheet Answers
Source: https://www.onlinemath4all.com/equations-of-circles-worksheet.html
Posted by: hillparented.blogspot.com

0 Response to "Writing Equations Of Circles Worksheet Answers"
Post a Comment